http://www.fisikastudycenter.com/fisika-xi-sma/30-momen-gaya-momen-inersia
Contoh Soal dan Pembahasan Momen Gaya dan Momen Inersia, Materi Fisika Kelas 11 (2) SMA. Contoh mencakup penggunaan rumus momen gaya, momen inersia untuk massa titik dan momen inersia beberapa bentuk benda, silinder pejal, bola pejal dan batang tipis.

Soal No. 1
Empat buah gaya masing-masing :
F1 = 100 N
F2 = 50 N
F3 = 25 N
F4 = 10 N
bekerja pada benda yang memiliki poros putar di titik P seperti ditunjukkan gambar berikut! Jika ABCD adalah persegi dengan sisi 4 meter, dan tan 53o = 4/3, tentukan besarnya momen gaya yang bekerja pada benda dan tentukan arah putaran gerak benda!

Pembahasan
Diagram gaya-gaya yang bekerja pada benda (tampak depan) sebagai gambar berikut :

Misal :
(+) untuk putaran searah jarum jam
(−) untuk putaran berlawanan arah jarum jam
(Ket : Boleh dibalik)

Sesuai perjanjian tanda di atas, benda berputar searah jarum jam
Soal No. 2
Empat buah gaya masing-masing :
F1 = 10 N
F2 = 10 N
F3 = 10 N
F4 = 10 N
dan panjang AB = BC = CD = DE = 1 meter

Dengan mengabaikan berat batang AE, tentukan momen gaya yang bekerja pada batang dan arah putarannya jika:
a) poros putar di titik A
b) poros putar di titik D
Pembahasan
a) poros putar di titik A

Putaran searah jarum jam.
b) poros putar di titik D

Putaran berlawanan arah dengan jarum jam

Pembahasan
Diagram gaya-gaya yang bekerja pada benda (tampak depan) sebagai gambar berikut :

Misal :
(+) untuk putaran searah jarum jam
(−) untuk putaran berlawanan arah jarum jam
(Ket : Boleh dibalik)

Sesuai perjanjian tanda di atas, benda berputar searah jarum jam
Soal No. 2
Empat buah gaya masing-masing :
F1 = 10 N
F2 = 10 N
F3 = 10 N
F4 = 10 N
dan panjang AB = BC = CD = DE = 1 meter

Dengan mengabaikan berat batang AE, tentukan momen gaya yang bekerja pada batang dan arah putarannya jika:
a) poros putar di titik A
b) poros putar di titik D
Pembahasan
a) poros putar di titik A

Putaran searah jarum jam.
b) poros putar di titik D

Putaran berlawanan arah dengan jarum jam
Soal No. 3
Batang AB = 2 meter dengan poros titik A dengan gaya F sebesar 12 N membentuk sudut 60°.

Tentukan besar momen gaya yang terjadi pada batang AB.
Pembahasan
Beberapa cara biasa digunakan diantaranya:
τ = F d sin α
τ = 12 (2) sin 60°
τ = 12 (2)(1/2 √3) = 12√3 Nm
Atau diuraikan dulu gaya F,

Yang menimbulkan torsi adalah F sin 60° dengan jaraknya ke A adalah 2 m, sementara F cos 60° mengakibatkan torsi sebesar NOL, karena jaraknya ke poros A adalah nol.
τ = F sin 60° (AB)
τ = 12 (1/2 √3)(2) = 12√3 Nm
Soal No. 4
Batang AC = 4 meter dengan poros titik A dengan gaya F1 sebesar 20 N dan F2 sebesar 12 N. Sudut-sudut ditunjukkan gambar berikut:

Jika titik B berada di tengah batang AC, tentukan besar momen gaya yang terjadi pada batang AC, dalam kasus ini massa batang diminta untuk diabaikan.
Pembahasan
Momen gaya dengan poros di titik A:
τ = F1 AC sin 60° − F2 AB sin 60°
τ = 20 (4) (1/2 √3) − 12 (2) (1/2 √3)
τ = 28√3 Nm
Soal No. 5
Susunan 3 buah massa titik seperti gambar berikut!

Jika m1 = 1 kg, m2 = 2 kg dan m3 = 3 kg, tentukan momen inersia sistem tersebut jika diputar menurut :
a) poros P
b) poros Q
Pembahasan
a) poros P

b) poros Q

Batang AB = 2 meter dengan poros titik A dengan gaya F sebesar 12 N membentuk sudut 60°.

Tentukan besar momen gaya yang terjadi pada batang AB.
Pembahasan
Beberapa cara biasa digunakan diantaranya:
τ = F d sin α
τ = 12 (2) sin 60°
τ = 12 (2)(1/2 √3) = 12√3 Nm
Atau diuraikan dulu gaya F,

Yang menimbulkan torsi adalah F sin 60° dengan jaraknya ke A adalah 2 m, sementara F cos 60° mengakibatkan torsi sebesar NOL, karena jaraknya ke poros A adalah nol.
τ = F sin 60° (AB)
τ = 12 (1/2 √3)(2) = 12√3 Nm
Soal No. 4
Batang AC = 4 meter dengan poros titik A dengan gaya F1 sebesar 20 N dan F2 sebesar 12 N. Sudut-sudut ditunjukkan gambar berikut:

Jika titik B berada di tengah batang AC, tentukan besar momen gaya yang terjadi pada batang AC, dalam kasus ini massa batang diminta untuk diabaikan.
Pembahasan
Momen gaya dengan poros di titik A:
τ = F1 AC sin 60° − F2 AB sin 60°
τ = 20 (4) (1/2 √3) − 12 (2) (1/2 √3)
τ = 28√3 Nm
Soal No. 5
Susunan 3 buah massa titik seperti gambar berikut!

Jika m1 = 1 kg, m2 = 2 kg dan m3 = 3 kg, tentukan momen inersia sistem tersebut jika diputar menurut :
a) poros P
b) poros Q
Pembahasan
a) poros P

b) poros Q

Soal No. 6
Bola A bermassa = 60 gram dan bola B = 40 gram dihubungkan batang AB (massanya diabaikan).

Jika kedua bola diputar dengan sumbu putar di P maka momen inersia sistem adalah….
A. 12,25 .10 –4 kg m2
B. 13,50 .10 –4 kg m2
C. 14,50 .10 –4 kg m2
D. 15,50 .10 –4 kg m2
E. 16,25 .10 –4 kg m2
(Momen Inersia - UN Fisika 2013)
Bola A bermassa = 60 gram dan bola B = 40 gram dihubungkan batang AB (massanya diabaikan).

Jika kedua bola diputar dengan sumbu putar di P maka momen inersia sistem adalah….
A. 12,25 .10 –4 kg m2
B. 13,50 .10 –4 kg m2
C. 14,50 .10 –4 kg m2
D. 15,50 .10 –4 kg m2
E. 16,25 .10 –4 kg m2
(Momen Inersia - UN Fisika 2013)
Pembahasan
Momen inersia di titik dengan sumbu putar di p

Soal No. 7
Lima titik massa tersusun seperti gambar berikut!

m1 = 1 kg, m2 = 2 kg , m3 = 3 kg, m4 = 4 kg, m5 = 5 kg
Tentukan momen inersianya jika:
a) poros putar sumbu X
b) poros putar sumbu Y
Pembahasan
a) poros putar sumbu X

b) poros putar sumbu Y

Soal No. 8
Tiga buah benda masing-masing :
Bola pejal massa 5 kg
Silinder pejal massa 2 kg
Batang tipis massa 0,12 kg
D = 2 m

Tentukan momen inersia masing- masing benda dengan pusat benda sebagai porosnya!
Pembahasan
Bola Pejal

Silinder Pejal
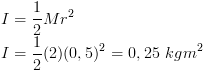
Batang Tipis

Soal No. 9
Diberikan sebuah batang tipis dengan panjang 4 meter dan bermassa 240 gram seperti gambar berikut:

Jika momen inersia dengan poros di pusat massa batang adalah I = 1/12 ML2 tentukan besar momen inersia batang jika poros digeser ke kanan sejauh 1 meter!
Pembahasan
Jika momen inersia dengan poros berada di pusat massa batang diketahui maka jika poros digeser sejauh x besar momen inersia yang baru adalah:
Momen inersia di titik dengan sumbu putar di p

Soal No. 7
Lima titik massa tersusun seperti gambar berikut!

m1 = 1 kg, m2 = 2 kg , m3 = 3 kg, m4 = 4 kg, m5 = 5 kg
Tentukan momen inersianya jika:
a) poros putar sumbu X
b) poros putar sumbu Y
Pembahasan
a) poros putar sumbu X

b) poros putar sumbu Y

Soal No. 8
Tiga buah benda masing-masing :
Bola pejal massa 5 kg
Silinder pejal massa 2 kg
Batang tipis massa 0,12 kg
D = 2 m

Tentukan momen inersia masing- masing benda dengan pusat benda sebagai porosnya!
Pembahasan
Bola Pejal

Silinder Pejal
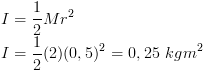
Batang Tipis

Soal No. 9
Diberikan sebuah batang tipis dengan panjang 4 meter dan bermassa 240 gram seperti gambar berikut:

Jika momen inersia dengan poros di pusat massa batang adalah I = 1/12 ML2 tentukan besar momen inersia batang jika poros digeser ke kanan sejauh 1 meter!
Pembahasan
Jika momen inersia dengan poros berada di pusat massa batang diketahui maka jika poros digeser sejauh x besar momen inersia yang baru adalah:
 |
dimana:
Ip = momen inersia saat poros di pusat massa
Ix = momen inersia jika poros digeser sejauh x dari pusat massa
M = massa batang
L = panjang batang
x = pergeseran poros dari pusat massa batang
Persamaan di atas dikenal sebagai teorema sumbu sejajar.
sehingga:


Soal No. 10
Sebuah gaya F bekerja pada bidang persegi dengan poros di titik P seperti gambar berikut.

Jika momen gaya yang diakibatkan oleh gaya F adalah τ = F d, tentukan nilai d yang dipergunakan untuk menghitung momen gaya tersebut!
Pembahasan
Menentukan jarak gaya terhadap poros

Sebuah gaya F bekerja pada bidang persegi dengan poros di titik P seperti gambar berikut.

Jika momen gaya yang diakibatkan oleh gaya F adalah τ = F d, tentukan nilai d yang dipergunakan untuk menghitung momen gaya tersebut!
Pembahasan
Menentukan jarak gaya terhadap poros

Garis putus-putus adalah perpanjangan gaya F, kemudian ambil garis d dari titik P sehingga tegak lurus dengan arah gaya atau perpanjangannya.
Dari gambar di atas diperoleh segitiga bantu yang jika ditegakkan seperti gambar berikut

Untuk menentukan d gunakan hubungan sudut dengan sisi-sisi segitiga, trigonometri:
d = PQ sin 37°
d = 2 (0,6) = 1,2 meter
Soal No. 11
Sebuah pipa dengan panjang L = 2 meter memiliki jari-jari luar pipa adalah 22 cm dengan jari-jari dalam 20 cm.

Jika massa pipa adalah 4 kg, tentukan momen inersia pipa!
Pembahasan
Momen inersia silinder berongga adalah sebagai berikut

R1 = 20 cm = 20/100 meter, R2 = 22 cm = 22/100 meter, M = 4 kilogram, sehingga


Untuk menentukan d gunakan hubungan sudut dengan sisi-sisi segitiga, trigonometri:
d = PQ sin 37°
d = 2 (0,6) = 1,2 meter
Soal No. 11
Sebuah pipa dengan panjang L = 2 meter memiliki jari-jari luar pipa adalah 22 cm dengan jari-jari dalam 20 cm.

Jika massa pipa adalah 4 kg, tentukan momen inersia pipa!
Pembahasan
Momen inersia silinder berongga adalah sebagai berikut

R1 = 20 cm = 20/100 meter, R2 = 22 cm = 22/100 meter, M = 4 kilogram, sehingga

Soal No. 12
Sebuah tongkat yang panjangnya 40 cm mendapat tiga gaya yang sama besarnya 10 newton seperti pada gambar.

Jika tongkat diputar di titik C, tentukan momen gaya total!
Sebuah tongkat yang panjangnya 40 cm mendapat tiga gaya yang sama besarnya 10 newton seperti pada gambar.

Jika tongkat diputar di titik C, tentukan momen gaya total!
Pembahasan
Momen gaya dengan pusat C, misal searah jarum jam diberi tanda (−) dan berlawanan arah jarum jam tanda (+).

Momen gaya dengan pusat C, misal searah jarum jam diberi tanda (−) dan berlawanan arah jarum jam tanda (+).

Soal No. 13
Batang AB panjang 100 cm, massa 3 kg dan tidak diabaikan. Pada batang bekerja gaya 20 N dan 10 N seperti gambar berikut!

Besar momen gaya dengan titik P sebagai porosnya adalah.....(gunakan percepatan gravitasi bumi g = 10 m/s2)
A. 2 Nm
B. 3 Nm
C. 4 Nm
D. 5 Nm
E. 6 Nm
Pembahasan
Karena massa batang tidak diabaikan, tambahkan satu gaya lagi yaitu gaya berat yang besarnya w = mg = 3 x 10 = 30 N. Letakkan dipusat massa dari benda dalam hal ini di tengah-tengah batang seperti gambar berikut!

Perlakukan gaya ini seperti dua gaya yang lain saat menghitung momen gaya.
Misal searah jarum jam tanda negatif, berlawanan positif (tanda boleh dibalik).

Hasilnya negatif, yang artinya sesuai pemberian tanda tadi, momen gaya searah jarum jam dan besarnya 5 Nm.
Batang AB panjang 100 cm, massa 3 kg dan tidak diabaikan. Pada batang bekerja gaya 20 N dan 10 N seperti gambar berikut!

Besar momen gaya dengan titik P sebagai porosnya adalah.....(gunakan percepatan gravitasi bumi g = 10 m/s2)
A. 2 Nm
B. 3 Nm
C. 4 Nm
D. 5 Nm
E. 6 Nm
Pembahasan
Karena massa batang tidak diabaikan, tambahkan satu gaya lagi yaitu gaya berat yang besarnya w = mg = 3 x 10 = 30 N. Letakkan dipusat massa dari benda dalam hal ini di tengah-tengah batang seperti gambar berikut!

Perlakukan gaya ini seperti dua gaya yang lain saat menghitung momen gaya.
Misal searah jarum jam tanda negatif, berlawanan positif (tanda boleh dibalik).

Hasilnya negatif, yang artinya sesuai pemberian tanda tadi, momen gaya searah jarum jam dan besarnya 5 Nm.
Soal No. 14
Sebuah batang homogen memiliki panjang 2 m. Kedua ujung batang dikenakan gaya seperti gambar berikut!

Tentukan besar momen kopel gaya pada batang!
Pembahasan
Kopel adalah pasangan dari dua buah gaya yang sama besar dan memiliki arah yang berlawanan. Besarnya momen kopel (M) dirumuskan:
Sebuah batang homogen memiliki panjang 2 m. Kedua ujung batang dikenakan gaya seperti gambar berikut!

Tentukan besar momen kopel gaya pada batang!
Pembahasan
Kopel adalah pasangan dari dua buah gaya yang sama besar dan memiliki arah yang berlawanan. Besarnya momen kopel (M) dirumuskan:
M = F d
dimana
F = besar salah satu gaya = 20 N
d = jarak kedua gaya = 2 m
sehingga
M = 20(2) = 40 Nm
dimana
F = besar salah satu gaya = 20 N
d = jarak kedua gaya = 2 m
sehingga
M = 20(2) = 40 Nm
Tidak ada komentar:
Posting Komentar